译者 | 陈峻

审校 | 重楼

不知您是否听说过积分神经网络（Integral Neural Networks，INN）。作为一种灵活的架构，它经由一次性训练，无需任何微调，便可被转换为任意用户指定的体积。由于声波（例如：音乐）可以被任何所需的采样率（也就是我们常说的：音质）进行采样，因此INN 可以动态地改变各种数据和参数形状（即：DNN质量）。

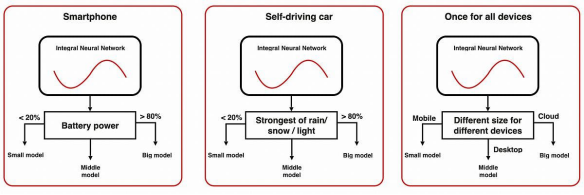
上图展示了INN的三种应用。在推理过程中，我们可以根据不同的硬件或数据条件，来动态改变网络的体积。这种体积的减小往往是结构化的，并且能够自动导致神经网络的压缩和加速。

TheStage.ai团队在今年的IEEE/CVF CVPR会议上展示了他们的论文《积分神经网络（Integral Neural Networks）》。该论文被认为是此次活动中12 篇仅有的“有望获奖”的论文之一。作为一类新型的神经网络，INN将连续参数和积分算子相结合，来表示各个基本层。在推理阶段，INN通过连续权重的离散采样，被转换为普通的DNN表示。由于此类网络的参数沿着过滤器和通道维度是连续的，因此这会导致结构化的修剪（pruning），而无需仅通过维度的重新离散化，而进行微调。

在下文中，我们将首先展示如何将4倍图像的超分辨率EDSR（Enhanced Deep Residual Networks for Single Image Super-Resolution）模型转换为INN的过程，然后演示如何实现针对模型的结构化修剪。在完成了将INN转换回离散的DNN后，我们通过将其部署到Nvidia GPU上，以实现高效的推理。总的说来，我们将按照如下顺序展开讨论：

1. 简介INN
2. 概述用于超分辨率任务的EDSR网络
3. 在一行代码中，通过TorchIntegral框架应用，获取积分的EDSR
4. 通过快速管道，实现无需INN微调的INN结构修剪
5. 在Nvidia GPU上部署已修剪的模型

首先，让我们有一个感性认识。上图展示的是离散的EDSR特征图。

而这张是则是INN EDSR的特征图。很容易看出INN中的通道是被连续组织的。

无需微调的DNN修剪

虽然INN中的各个层面已被积分算子所取代，但是对于积分算子的实际评估，我们需要对输入的信号进行离散化，以便采用数值积分的方法。同时，INN中的各个层次的设计方式是与离散化后的经典DNN层（如：全连接或卷积）保持一致的。

上图展示了积分全连接层评估的简要过程。

4倍图像的超分辨率EDSR的修剪

在基于扩散模型和Transformer的高端神经网络等架构中，我们往往需要用到图像超分辨率任务。它是一项被广泛使用的计算机视觉任务，往往被用在通过已知或未知的退化算子，来增强图像。其典型应用场景莫过于使用双立方下采样（Bicubic Downsampling），来作为退化算子的经典超分辨率形式。由于EDSR 架构包含了 ResNet（残差神经网络，目前被广泛地用于各类深度学习问题）和最终的4倍上采样块，非常适合我们后续的演示，因此我们将重点关注4倍EDSR架构。

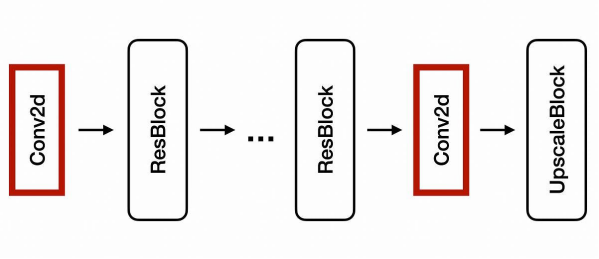
上图展示了EDSR的逻辑架构。该架构由一系列紧接着上采样块的残差块（Residual Blocks）所组成。此处的上采样块则是由多个卷积和上采样（Upsample）层组成。

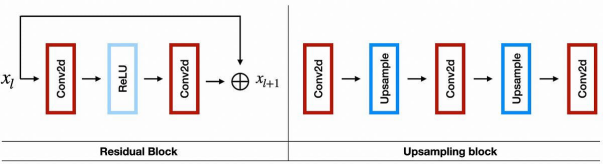
在上图中，左侧是：残差块的架构；而右侧是：4倍超分辨率的上采样块。其中，每个上采样层都有2倍的规模。

EDSR架构的修剪细节

结构化的修剪往往涉及删除整个过滤器或通道，进而对作为EDSR中主要构建块的残差块，产生独特的影响。而在该架构中，由于每个状态都是通过向输入添加Conv -> ReLU -> Conv块来更新的，因此输入和输出信号必须具有相同数量的参数。那么通过创建修剪依赖关系图，我们便可以在TorchIntegral框架中有效地管理这些。下图展示了每个残差块的第二卷积，是如何形成单个组的。

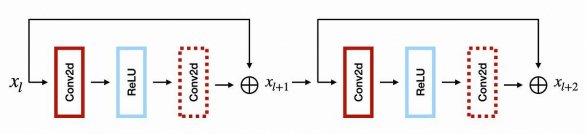
也就是说，为了修剪残差块中的第二卷积，我们有必要修剪每个残差块中的所有第二卷积。当然，为了更灵活的设置，我们实际上应该在所有残差块中，修剪第一卷积的过滤器，从而实现对第二卷积通道的修剪。

将EDSR模型转换为INN EDSR

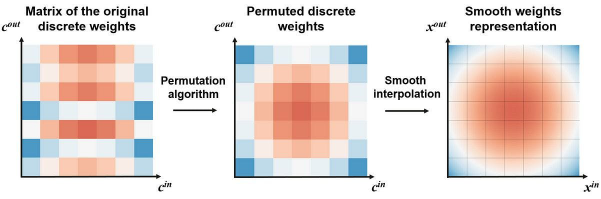
接着，为了实现针对预训练的DNN转换，我们需要利用特殊的过滤器通道排列算法，进一步平滑插值（interpolation）。此类排列算法不但能够保留模型的质量，而且会使得DNN的权重，看起来像是从连续函数中采样出来的一样。

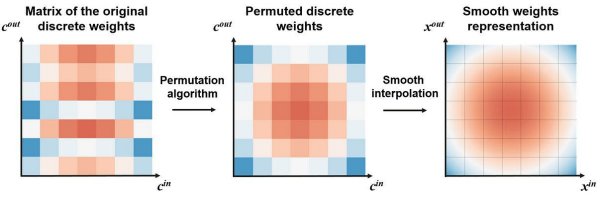
上图展示了从DNN到INN 的转换。我们使用著名的“旅行推销员问题（Travelling Salesman Problem，即：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。）”公式，来排列各个离散的权重。在完成排列后，我们将获得更平滑的权重，同时它也保证了预训练DNN的质量不会下降。具体请参见如下代码段：

import torch
import torchintegral as inn
from super_image import EdsrModel

# creating 4x EDSR model
model = EdsrModel.from_pretrained("eugenesiow/edsr", scale=4).cuda()

# Transform model layers to integral.
# continous_dims and discrete dims define which dimensions
# of parameters tensors should be parametrized continuously
# or stay fixed size as in discrete networks.
# In our case we make all filter and channel dimensions
# to be continuous excluding convolutions of the upsample block.
model = inn.IntegralWrapper(init_from_discrete=True)(
 model, example_input, continuous_dims, discrete_dims
).cuda()

积分网格调整：DNN结构化训练的后期修剪

所谓积分网格调整（Integration grid tuning），是指在SGD（随机梯度下降）的优化过程中，平滑地选择参数张量（parameter tensors）的操作。其过滤器应针对由用户定义的数字，来进行采样。与上述过滤器和通道删除方法不同，由INN生成的过滤器，可以通过插值操作，来组合多个离散过滤器。注意，INN在过滤器和通道维度的参数张量上，引入了软按索引选择（soft select-by-index）的操作。具体请参见如下代码段：

# Set trainable gird for each integral layer
# Each group should have the same grid
# During the sum of continuous signals
# We need to sample it using the same set of points

for group in model.groups:
 new_size = 224 if 'operator' in group.operations else 128 
 group.reset_grid(inn.TrainableGrid1D(new_size))

# Prepare model for tuning of integration grid
model.grid_tuning()
# Start training
train(model, train_data, test_data)

由于积分网格调整是一种快速的优化过程，可以在小型校准集上进行，因此其优化结果便是已在结构上压缩了的DNN。我们在单颗 Nvidia A4000 上的测试表明：对完整的Div2k数据集的积分网格进行调整，通常需要4分钟。 那么，在四倍A4000上的分布式设置，就能够几乎实现4倍的加速，其优化时间将仅为1分钟。

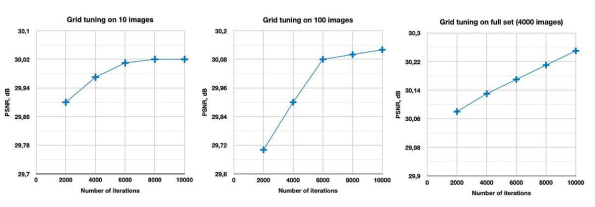
如上图所示，在实验中，我们发现：500张图片与包含4000张图片的完整训练集 Div2k，所给出的结果是相同的。

性能

如果我们需要将修剪后的INN模型转换为离散模型，则可以使用以下代码行：

model = model.transform_to_discrete()
# then model can be compiled, for instance
# compilation can add an additional 1.4x speedup for inference
model = torch.compile(model, backend='cudagraphs')

当输入的分辨率为64x64时，我们便可以在RTX A4000上提供每秒帧数(FPS)了。可见，上文生成的INN模型可以被轻松转换为离散模型，并被部署在任何NVIDIA GPU上。至此，已压缩的模型几乎实现了2倍的加速度。

如上图所示，左侧是4倍双立方放大图像；右侧则是使用INN的经50%压缩的EDSR模型。下表展示了更详细的对比：

小结

在上文中，我们简述了《积分神经网络》一文的基本成果：凭借着4倍EDSR模型的训练后修建，我们仅通过单行代码和1分钟的积分网格微调，便实现了近2倍的加速度。针对上述话题，您可以通过查看如下资源，以获取更多有关高效模型部署的信息与更新。

1. INN项目站点--https://inn.thestage.ai/?ref=hackernoon.com
2. INN 项目的Github资源--https://github.com/TheStageAI/TorchIntegral?ref=hackernoon.com
3. 与本文相关的支持代码--https://github.com/TheStageAI/TechBlog/tree/main/inn_edsr_grid_tuning_medium?ref=hackernoon.com

译者介绍

陈峻（Julian Chen），51CTO社区编辑，具有十多年的IT项目实施经验，善于对内外部资源与风险实施管控，专注传播网络与信息安全知识与经验。

原文标题：Unleashing 2x Acceleration for DNNs: Transforming Models with Integral Neural Networks in Just 1 Min，作者：thestage